Zeus Reversi

An artificial intelligence of Reversi Game based on Monte-Carlo Tree Search.

Won the championship of 2018 AI Reversi Match at Zhejiang University, China.

Here is a demo showing how to play with it.

This project contains 18K lines of C++ code.

Reversi Game

Each of the disks’ two sides corresponds to one player; they are referred to here as light and dark after the sides of Othello pieces, but any counters with distinctive faces are suitable. The game may for example be played with a chessboard and Scrabble pieces, with one player letters and the other backs.

The game begins with four disks placed in a square in the middle of the grid, two facing white-side-up, two dark-side-up, so that the same-colored disks are on a diagonal. The dark player moves first.

Dark must place a piece (dark-side-up) on the board and so that there exists at least one straight (horizontal, vertical, or diagonal) occupied line between the new piece and another dark piece, with one or more contiguous light pieces between them.

Play always alternates. After placing a dark disk, dark turns over (flips to dark, captures) the single disk (or chain of light disks) on the line between the new piece and an anchoring dark piece. No player can look back to the previous status of disks when playing moves. A valid move is one where at least one piece is reversed (flipped over).

For more information, check wiki for Reversi

Monte Carlo Tree Search

Monte Carlo tree search (MCTS) is a heuristic search algorithm for some kinds of decision processes, most notably those employed in software that plays board games. In that context MCTS is used to solve the game tree.

For more information, check wiki for MCTS

My Implementation

Node Quality

For Reversi Game, it is vital to import some human intelligence. So I import another dimension in the UCB formula to evaluate the ‘score’ of a child node. The improved UCB formula is as the following.

To calculate the quality of a child node, I found some evaluation from the paper of the World-wide Reversi Champion of 2001, Brian Rose: Othello: A Minute to Learn. A Lifetime to Master.

He says, to evaluate whether a move is good or not, we shall focus on the following features of the board.

• Corner: location A1, A8, H1, H8 on the board, where the piece on it cannot be flipped.
• Stable discs: the pieces can definitely not be flipped.
• Frontier: the pieces placed next to at least an empty location.
• Mobility: the number of valid moves for one side.
• Potential: the number of valid moves for both sides,
• Parity: the parity of distance from a frontier piece to the border of the board.
• Quiet Move: a move which does not flip a frontier piece, which is usually a good one.

Overall strategy

We refer to AlphaGo’s paper and learned that it has a trained network to select the next step in the tree policy stage; in the default policy stage, AlphaGo handles the trade-off between speed and accuracy well, using local feature matching and linear regression; the icing on the cake is that AlphaGo has adopted a deep convolutional network to estimate the board. Restricted by the hardware, it is impossible for me to fully replicate its approach, but it does not prevent me from analyzing its strategy and extracting the parts that may be effective for my task.

I believe that the performance of Monte Carlo Tree Search depends on two factors, one is the accuracy of selecting the best child node in the tree policy stage, and the other is the strength of the default policy.

If the tree policy is powerful, it is more likely to constrain the growth direction of the tree to the direction of the optimal solution.

If the default policy is strong, the confidence of the winning rate is higher. The strong here means the number of simulations that can be performed and how performance in one run is optimized.

AlphaGo’s handling of these two problems is that for problem one, it uses a trained network to give an estimate of all possible positions of the next hand. The training data comes from a large number of human games and game records obtained through reinforcement learning.

For the second problem, it is too slow to use neural network again. It draws on some human knowledge of Go, extracts features of the board and scores each feature, and finally uses linear regression to get the total score. It also uses a deep convolutional network to reduce the search breadth.

My final strategy is as follows:

1. As the game begins, first import the game record of human experts and construct an opening tree. For each move, the opening tree is searched for whether there is a match. We keep use the opening tree until there is no match for the current board.
2. At about 12 steps to the last move, start position evaluation. Position evaluation is to extract the local features of a board, such as the distribution of pieces on each side, corner, and diagonal. And use the pre-trained parameters to predict the final outcome of the current board. I used a large number of human game records with a linear regression model to determine the score of each local feature and their respective weights.
3. Use the minimum and maximum tree in the first three steps of each search, and select the best move according to the quality of the board. And then use Monte Carlo tree simulation. So the quality evaluation works as another heuristic search algorithm.
4. When each round of Monte Carlo simulation is about 12 steps away from the endgame, the result of position evaluation is used instead of the final result to return. In order to avoid the influence of randomness, the backpropagation is a piecewise function. The segment is given: For example, if you can only win within 5, it returns 0.5, and if you can win between 5 and 10, it returns 0.8. Only estimated to win more than 15, it returns 1.
5. When the game progresses to about 18 moves before the board is filled, the above search method is completely abandoned, and the minimum and maximum tree based on the parity judgment is used to determine the next move, because there are not many spaces left. At that time, the end game of the board can already be searched within the time allowed.

Memory Pool

During the growth of the Monte Carlo tree, it is necessary to dynamically allocate and deallocate nodes. If it continuously dynamically allocate memory, it will not only affect the search efficiency, but may also cause space leakage. So I adopt a memory pool mechanism to manage all unused memory in a linked list, and use child threads to process the nodes that need to be deleted into the memory pool linked list.

Multi-thread Computing

Each run in the Monte Carlo tree search is almost independent, which provides possibility for the parallel implementation. After careful analysis, I divide all operations that may affect parallelism into three levels, which are natural parallelism, possible parallelism, and must be locked. Natural parallelism means that the operation is originally a local variable operation on the thread, and multiple threads do not affect each other, and there is no need to add thread locks; parallel operation means that the operations between multiple threads will interfere with each other, but interfere with the final search The result has little effect. You can choose to make it parallel under the consideration of efficiency. This operation appears when calculating the score value. In the “selection” step, when the score of each node is being calculated, the winning rate and the number of visits of some nodes are affected. In the case of updates, this will affect the accuracy of our score calculation, but when the total number of searches is large enough, the impact of this deviation on the chess power can be ignored; the last is the operation that must be locked, if the lock is not performed It may happen that the program crashes and access is abnormal, and we have to lock the operation.

In the end, found that only when a new node is generated, because the memory needs to be dynamically allocated, there is only one entry for allocating memory (must be allocated from the root node of the memory pool linked list), and to prevent multiple threads from trying to the same node The situation of applying for memory space. This process must be locked, and the code of the final locking part is as follows.

Template Match

I use template match for position evaluation. The entire chessboard is decomposed into 46 areas, and the local chess shape of the estimated chessboard is checked area by area. Different types of areas are used when calculate the position evaluation of different dimensions. For example, the template configuration for calculating the action force is line segments of different lengths horizontally, vertically and obliquely on the board, while the template for the stabilizer and corner configuration is the shape of the chess pieces gathered at the corners.

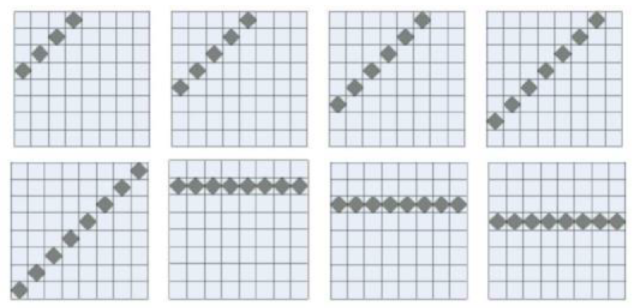
The template data is extracted by a linear regression model combined with the data of 70,000 games. The calculated results are stored in a linear table. When evaluating, only the linear combination of the number of these templates needs to be calculated. This operation is basically to read The memory is used for implementation, which is extremely efficient and has considerable accuracy, so it can support Monte Carlo tree search result estimation.